|
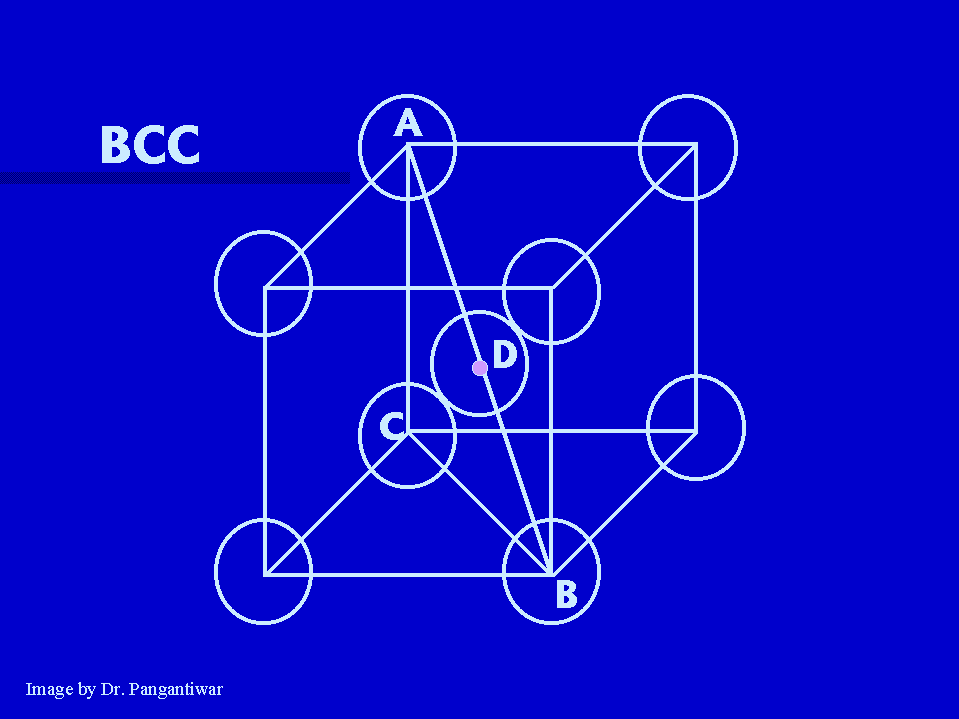
In BCC nearest neighbours are atoms at A and D. |
Miller indices are the reciprocals of the intercepts, made by the plane on the crystallographic axes, when reduced to smallest integers.
Miller indices are used to designate the planes in a crystal lattice.
Intecepts on x, y and z axes :- 1, 2, infinity
The reciprocals of intercepts :- 1/1, 1/2, 1/infinity
i.e. 1/1, 1/2, 0
Reciprocals are reduced to smallest set of integers by taking LCM :- 2, 1, 0
So, miller indices :- (2,1,0)
FOR BCC
i) Number of atoms per unit cell :- (8 x 1/8) + 1 = 2.
ii) The co-ordination number :- 8, because there are eight unit cells surrounding a corner atom in BCC unit cell. Atom at the centre of the unit cell is nearest to the corner atom in unit cell.
iii) The packing fraction :- 2 x (4/3) PI (R)3 / (a)3
i.e. 2/1 x 4/3 x PI/1 x [(square root of 3) x a /4]3 x 1/ (a)3
i.e. (square root of 3) x (PI / 8)
i.e. 0.68
GIVEN :-
Lamda = 1.54 Angstrom = 1.54 x 10-10 m.
Theta = 22.4 degrees.
Spacing of (2,0,0) planes in Aluminium = d = [a / square root of ( 22 + 0 + 0 )] i.e a / 2.
a = ?
2d sin(theta) = n Lamda
i.e. 2 x (a/2) x sin(22.4) = 1 x 1.54 x 10-10
i.e. a = (1.54 x 10-10) / (0.3811)
i.e. a = 4.04 A0
The packing fraction in FCC :-
4 x (4/3) PI (R)3 / (a)3
i.e. 4/1 x 4/3 x PI/1 x [(square root of 2) x a /4]3 x 1/ (a)3
i.e. PI / (3 x square root of 2)
i.e. 0.74.
The packing fraction in BCC :-
2 x (4/3) PI (R)3 / (a)3
i.e. 2/1 x 4/3 x PI/1 x [(square root of 3) x a /4]3 x 1/ (a)3
i.e. (square root of 3) x (PI / 8)
i.e. 0.68.
i.e. packing fraction in FCC is more than in the BCC structure.
For the given crystal, it is possible to obtain experimentally the glancing angles for the maxima of reflected X-rays respectively using three different reflecting planes.
For example, In case of KCL crystal, Bragg obtained the first order of maximum of reflected X-rays at glancing angles 5.22 degrees, 7.30 degrees and 9.05 degrees respectively using three different reflecting planes.
From Bragg’s equation 2d sin(theta) = n Lamda
So, for first order spectrum 2d sin(theta) = Lamda
i.e. 1/d = 2 sin (theta) / Lamda
Thus, knowing the values of theta for reflections from different reflecting planes in given crystal and lamda, it is possible to find the ratio 1/d100 : 1/d110 : 1/d111and from this ratio, it is possible to analyse the given crystal structure.
For example for KCL crystal,
1/d1 : 1/d2 : 1/d3 :: sin 5.22 : sin 7.30 : sin 9.05
i.e. 1/d1 : 1/d2 : 1/d3 :: 0.091 : 0.127 : 0.157
i.e. 1/d1 : 1/d2 : 1/d3 :: 1: 1.4 : 1.73
This result shows that KCL is simple cubic crystal.
In this way Bragg’s law is useful in the analysis of the crystal structures.
The packing fraction in SC :-
1 x (4/3) PI (R)3 / (a)3
i.e. 1/1 x 4/3 x PI/1 x [a /2]3 x 1/ (a)3
i.e. PI / 6
i.e. 0.52
The packing fraction in BCC :-
2 x (4/3) PI (R)3 / (a)3
i.e. 2/1 x 4/3 x PI/1 x [(square root of 3) x a /4]3 x 1/ (a)3
i.e. (square root of 3) x (PI / 8)
i.e. 0.68.
The packing fraction in FCC :-
4 x (4/3) PI (R)3 / (a)3
i.e. 4/1 x 4/3 x PI/1 x [(square root of 2) x a /4]3 x 1/ (a)3
i.e. PI / (3 x square root of 2)
i.e. 0.74.
Hence the FCC structure possesses maximum packing density among the three crystal structures SC, BCC and FCC.
GIVEN :-
r = 1.68 A0 = 1.68 x 10-10 m.
Lattice system = SC
M = 209 kg / k. mol
N = 6.02 x 1026 atoms / k. mol.
For SC, r = a/2
So a = 2r = 2 x 1.68 x 10-10 m = 3.36 x 10-10 m
and n = 1
So Density = nM / N (a)3
= [( 1 atom) (209 kg / k. mol)] / [(6.02 x 1026 atoms / k. mol) (3.36 x 10-10m)3]
= [(209 / 228.34)] x 104 kg / m3
= 9150 kg / m3
Space lattice is defined as an array of points arranged in regular periodic fashion in three dimensional space such that each point in the lattice has exactly identical surrounding. The points are called lattice points or lattice sites.
A crystal structure is a space lattice in which the lattice sites are occupied by atoms or clusters of atoms. Each lattice point is associated with the same unit of groups of atoms, called the basis. The basis must be identical in composition, arrangement and orientation such that the crystal appears exactly the same at one point as it does at other equivalent points. When the basis is associated with each lattice site, the crystal structure is obtained.
Thus Space lattice + Basis = Crystal structure.
FOR BCC
i) Number of atoms per unit cell :- (8 x 1/8) + 1 = 2.
ii) The co-ordination number :- 8, because there are eight unit cells surrounding a corner atom in BCC unit cell. Atom at the centre of the unit cell is nearest to the corner atom in unit cell.
iii) The packing fraction :- 2 x (4/3) PI (R)3 / (a)3
i.e. 2/1 x 4/3 x PI/1 x [(square root of 3) x a /4]3 x 1/ (a)3
i.e. (square root of 3) x (PI / 8)
i.e. 0.68
GIVEN :-
Lattice system = FCC
Edge of unit cell, a = 3.52 A0 = 3.52 x 10-10 m
M = 58.71 kg / k. mol
N = 6.02 x 1026 atoms / k. mol.
and For FCC, n = 4
Density = nM / N (a)3
= [( 4 atoms) (58.71 kg / k. mol)] / [6.02 x 1026 atoms / k. mol) (3.52 x 10-10m)3]
= [(234.84 / 262.56)] x 104 kg / m3
= 8944 kg / m3

|
In BCC nearest neighbours are atoms at A and D. |
|
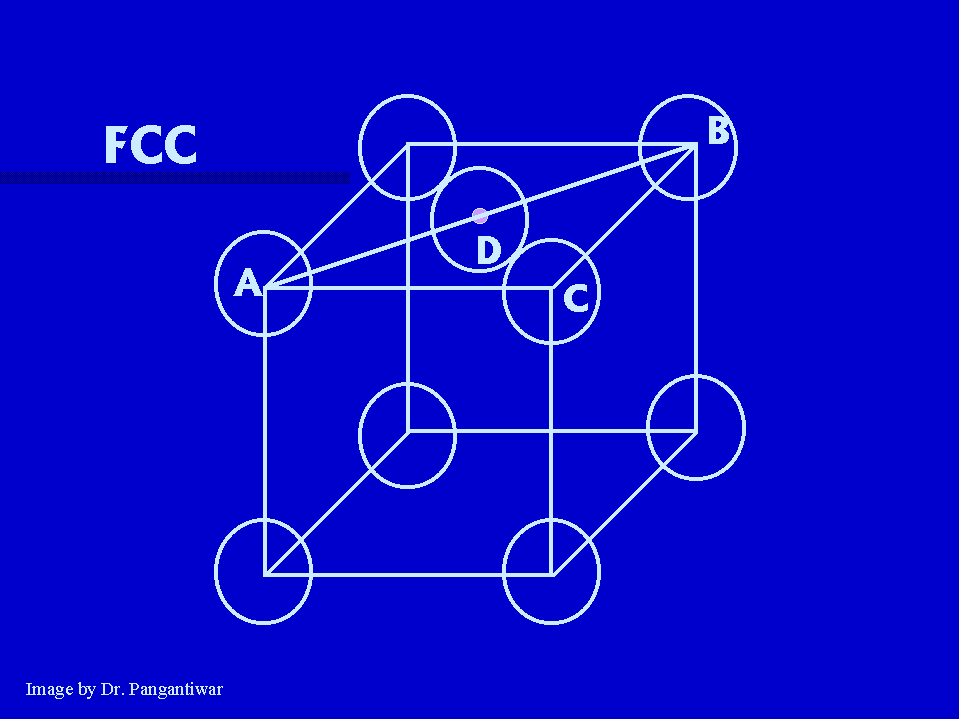
In FCC nearest neighbours are atoms at A and D. |
Miller indices are the reciprocals of the intercepts, made by the plane on the crystallographic axes, when reduced to smallest integers.
Miller indices are used to designate the planes in a crystal lattice.
|
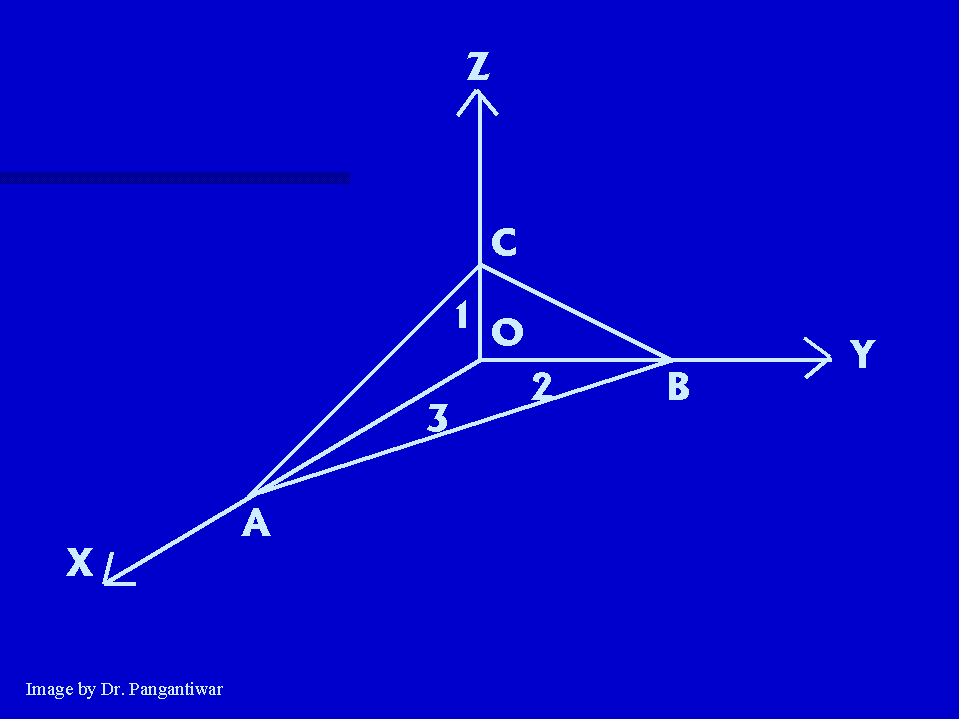
The intercepts are OA, OB, OC i.e. 3, 2, 1 The reciprocals of intercepts are 1/3, 1/2, 1/1 Taking LCM we get 2, 3, 6 So the miller indices of plane ABC are (2,3,6) |
GIVEN :-
r = 1.44 A0 = 1.44 x 10-10 m.
For FCC, a = 2 (square root of 2) r
i.e. a = 2 x 1.414 x 1.44 x 10-10 m
i.e. a = 4.07 x 10-10m
Spacing of (111) plane = d111 = [a / square root of ( h2 + k2 + l2 )]
i.e. d111 = [ 4.07 x 10-10 / square root of ( 12 + 12 + 12 )]
i.e. d111 = 2.35 x 10-10m.
We know that, 2d sin(theta) = n Lamda
i.e.2 x 2.35 x 10-10 x sin (32.1) = 1 lamda
So, lamda = 2.498 x 10-10m
Cubic crystal structure FCC has closest packing of atoms.
An atom in this type of crystal have 12 nearest neighbours.

|
In FCC nearest neighbours are atoms at A and D. |
GIVEN :-
Lattice constant, a = 2.87 A0 = 2.87 x 10-10 m.
Lattice system = BCC
Density = 7870 kg / m3
N = 6.02 x 1026 atoms / k. mol.
For BCC, n = 2 atoms
Density = nM / N (a)3
So, atomic mass, M = (Density) N (a)3 / n
i.e. M = [(7870 kg/m3) (6.02 x 1026 atoms / k. mol) (2.87 x 10-10 m)3] / 2 atoms
i.e. M = 56 kg / k.mol
2d sin (theta) = n (lamda),
where d is the interplaner distance, (theta) is the angle between the Bragg plane and the direction of the incident beam and n = 1, 2, 3 ......... etc., for first order, second order, third order ...... etc., maxima respectively, is known as Bragg's law.
Let us consider a set of parallel lattice planes of a crystal seperated by a distance d apart, i.e. AB = d. Suppose a narrow beam of X-rays of wavelength (lamda) be incident upon these planes at an angle (theta) as shown in figure. The beam will be reflected in all directions by the atoms of various atomic planes. Because the refractive index of the matter of the crystal is very nearly equal to unity, there is practically no bending of the rays entering or leaving the crystal.

|
Consider a ray PA reflected at atom A in the direction AR from plane KL and another ray QB reflected at another atom B from plane MN in the direction BS. Now from the atom A, draw two perpendiculars AC and AD on the incident ray QB and reflected ray BS respectively. The path difference between these two rays is (CB+BD). The two reflected rays will be in phase or out of phase, will depend upon this path difference. When the path difference (CB+BD) is an integral multiple of the wavelength (lamda), then the |
two reflected rays will reinforce each other and produce an intense spot. Thus the condition of reinforcement is CB + BD = n (lamda)
From figure,
angle PAT = angle QTK = theta
But angle PAC = 900
So, angle TAC = 90 - theta
Now angle TAB = 900
So, as angle TAC = 90 - theta, angle CAB = theta
Now in right angled triangle ACB,
sin (angle CAB) = sin (theta) = CB / AB = CB / d
So, CB = d sin (theta).
Similarly, it can be shown that BD = d sin (theta)
So, CB + BD = 2d sin (theta) = n (lamda)
where n = 1, 2, 3 ......... etc., for first order, second order, third order ...... etc., maxima respectively. This relation is known as Bragg's law.
Intecepts on x, y and z axes :- a, 2a, 3a
The reciprocals of intercepts :- 1/a, 1/2a, 1/3a
Reciprocals are reduced to smallest set of integers by taking LCM :- 6, 3, 2
So, miller indices :- (6,3,2)
Now we have to draw (1,2,0) plane. Let intecepts by this plane on x, y and z axes are OA, OB

|
and OC. The reciprocals of intercepts :- 1/OA, 1/OB, 1/OC Reciprocals are reduced to smallest set of integers by taking LCM :- a/OA, a/OB, a/OC But, miller indices of this plane are:- (1,2,0) So, 1 = a/OA, 2 = a/OB, 0 = a/OC So, OA = a, OB = a/2 and OC = infinity i.e plane is parallel to z axis. i.e. OA = 2a, OB = 1a and plane is parallel to z axis. or, OA = 2, OB = 1 and plane is parallel to z axis. |
The packing density (PD) in SC :-
1 x (4/3) PI (R)3 / (a)3
i.e. 1/1 x 4/3 x PI/1 x [a /2]3 x 1/ (a)3
i.e. PI / 6
i.e. 0.52
The percentage of void space in SC :-
(1 - PD) x 100
i.e. (1 - 0.52) x 100 = 48%
The packing density in BCC :-
2 x (4/3) PI (R)3 / (a)3
i.e. 2/1 x 4/3 x PI/1 x [(square root of 3) x a /4]3 x 1/ (a)3
i.e. (square root of 3) x (PI / 8)
i.e. 0.68.
The percentage of void space in BCC :-
(1 - PD) x 100
i.e. (1 - 0.68) x 100 = 32%
The packing density in FCC :-
4 x (4/3) PI (R)3 / (a)3
i.e. 4/1 x 4/3 x PI/1 x [(square root of 2) x a /4]3 x 1/ (a)3
i.e. PI / (3 x square root of 2)
i.e. 0.74.
The percentage of void space in FCC :-
(1 - PD) x 100
i.e. (1 - 0.74) x 100 = 26%
Hence the FCC structure possesses maximum packing density and minimum percentage of void space among the three crystal structures SC, BCC and FCC.
Density = n M / N (a)3
So, for SC, where n = 1,
Density = M / N (a)3
So, for BCC, where n = 2,
Density = 2M / N (a)3
So, for FCC, where n = 4,
Density = 4M / N (a)3
GIVEN :-
Interplaner spacing, d = 2.82 A0 = 2.82 x 10-10 m.
Order of spectrum, n = 1
We know that, Bragg's law is 2d sin(theta) = n Lamda
For lamda to be maximum, theta = 900
So, lamda = 2d for first order longest wavelength
So, lamda = 2 x 2.82 A0 = 5.64 A0
(i) The relation between atomic radius (r) and unit cell dimension (a) for FCC structure is
r = a / [2(square root of 2)].
(ii) The coordination number for a typical BCC structure is 8.
(iii) The atomic packing fraction for a simple cubic structure is PI/6 = 0.52.
(iv) The percent void space for the BCC structure is 32%.
GIVEN :-
Lattice system = FCC
Density = 2180 kg / m3
Atomic weight of Na, M1 = 23 kg / k.mol
Atomic weight of Cl, M2 = 35.5 kg / k.mol
N = 6.02 x 1026 atoms / k. mol.
For FCC, n = 4 atoms
Density = nM / N (a)3
And weight of NaCl molecule = M1 + M2
So, a3 = n (M1 + M2) / (Density) N
i.e. a3 = [(4 atoms) (23 + 35.5) kg / k.mol] / [(2180 kg / m3) (6.02 x 1026 atoms / k. mol)]
i.e. a3 = 234 x 10-31 m3 / 1.31
i.e. a3 = 178.63 x 10-30 m3
So, Lattice constant, a = cube root of [178.63 x 10-30 m3]
i.e. a = 5.63 A0
So the distance between adjacent atoms, sodium and chlorine is, d = a /2
i.e. d = (5.63 / 2) A0 = 2.815 A0
Miller indices are the reciprocals of the intercepts, made by the plane on the crystallographic axes, when reduced to smallest integers.
Miller indices are used to designate the planes in a crystal lattice.
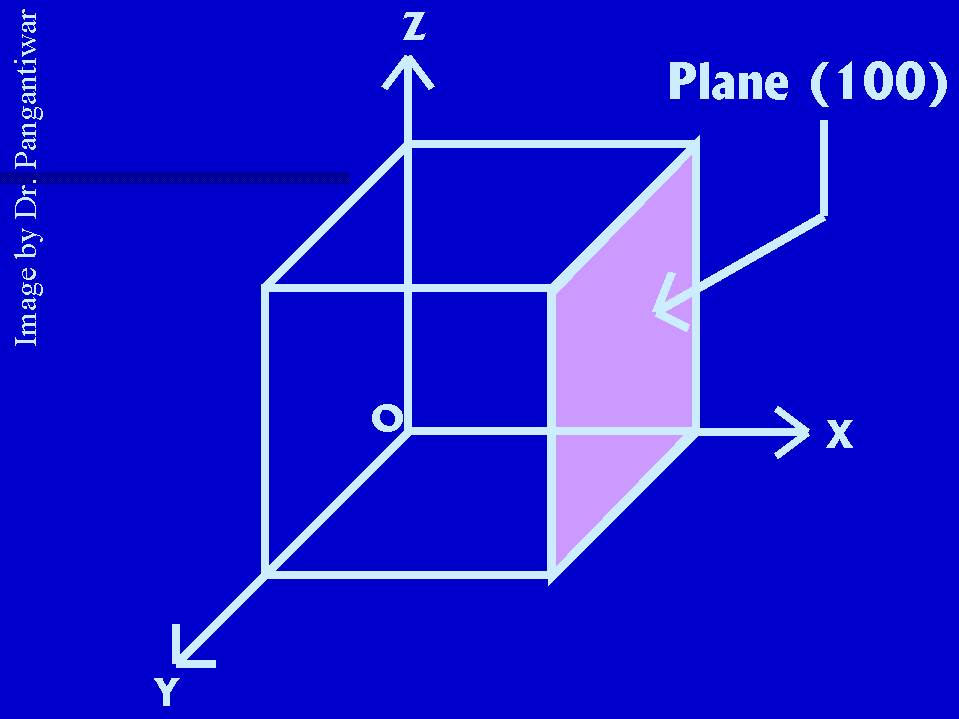
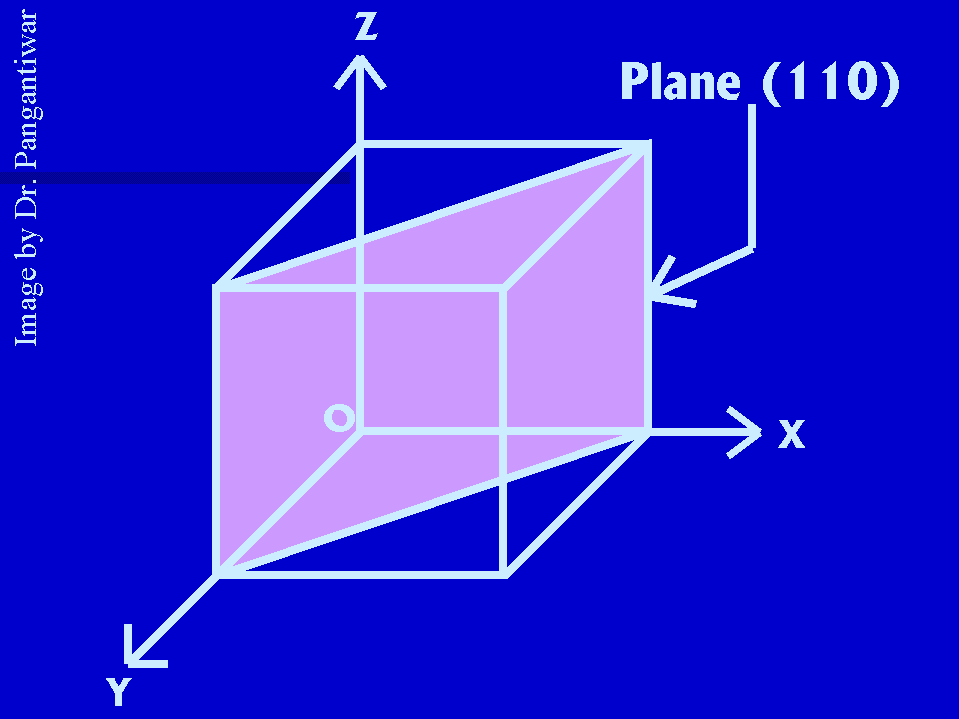
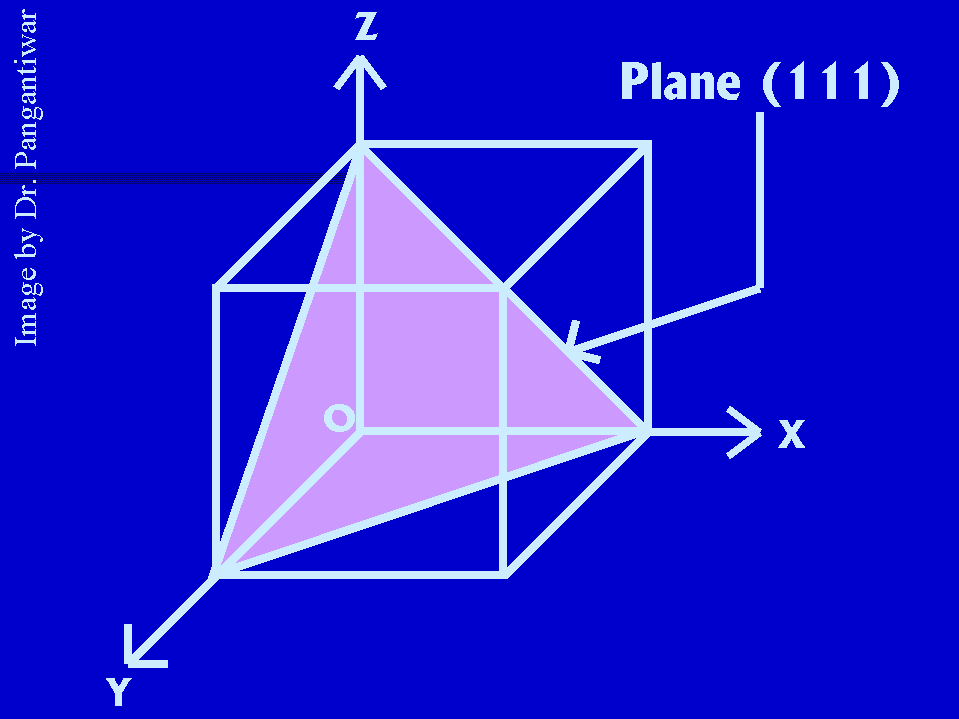
Let dhkl represent the distance between two adjacent parallel planes having Miller indices (hkl). Let the plane ABC be one of the planes. The perpendicular ON in figure from the origin to the plane ABC is equal to dhkl. Let ON makes angles alpha, beta and gama with x, y and z axes respectively. The intercepts of the plane ABC on the coordinate axes x, y and z are OA, OB and OC respectively.
Intercepts made by plane ABC on coordinate axes = OA, OB, OC
Reciprocals of these intercepts are = 1/OA, 1/OB, 1/OC
Taking LCM, we get a/OA, a/OB, a/OC
So Miller indices h = a/OA, k = a/OB, l = a/OC
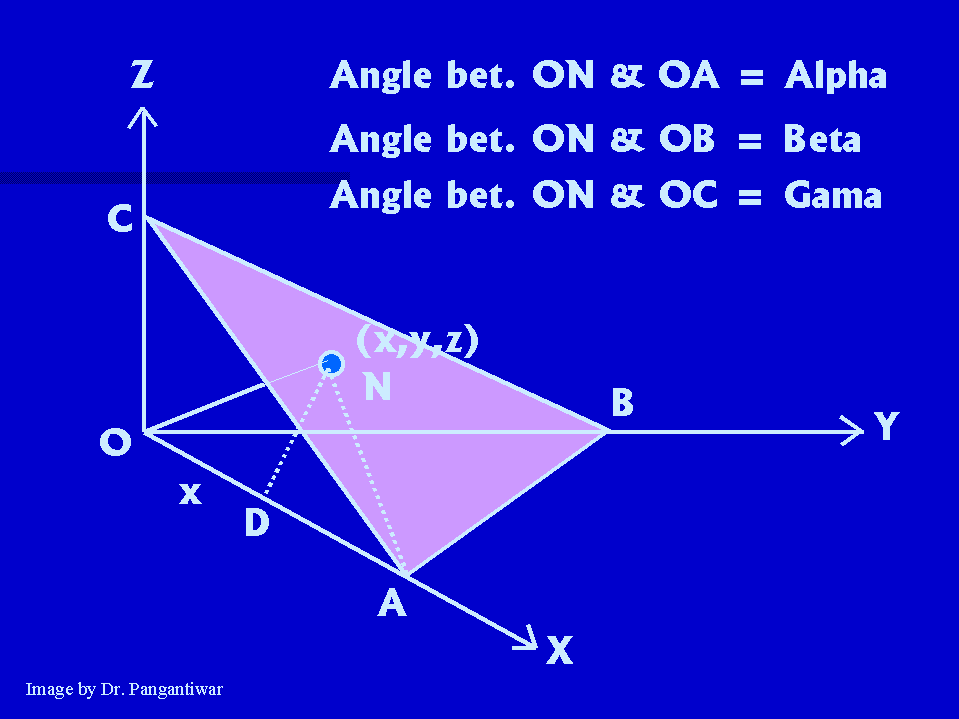
|
i.e. intercepts OA = a/h, OB = a/k, OC = a/l. |
So (dhkl)2 = d2 = d2 cos2(alpha) + d2 cos2(beta) + d2 cos2(gama)
i.e. cos2(alpha) + cos2(beta) + cos2(gama) = 1 ……… (1)
The points N and A lie in the plane ABC and ON is perpendicular to plane ABC. So ON is perpendicular to NA.
Now consider right angled triangle ONA. Here angle ONA is 90 degrees.
So, here cos (alpha) = d/OA = dh/a
Similarly cos (beta) = dk/a and cos (gama) = dl/a.
So, putting these values in equation (1), we get
(dh/a)2 + (dk/a)2 + (dl/a)2 = 1
i.e. [d2/a2] ( h2 + k2 + l2 ) = 1
i.e. d2 = a2/ ( h2 + k2 + l2 )
i.e. dhkl = a / [square root of ( h2 + k2 + l2)]


i.e. we have to obtain the expression for Bragg's law, 2d sin (theta) = n (lamda),
where d is the interplaner distance, (theta) is the angle between the Bragg plane and the direction of the incident beam and n = 1, 2, 3 ......... etc., for first order, second order, third order ...... etc., maxima respectively.
Let us consider a set of parallel lattice planes of a crystal seperated by a distance d apart, i.e. AB = d. Suppose a narrow beam of X-rays of wavelength (lamda) be incident upon these planes at an angle (theta) as shown in figure. The beam will be reflected in all directions by the atoms of various atomic planes. Because the refractive index of the matter of the crystal is very nearly equal to unity, there is practically no bending of the rays entering or leaving the crystal.

|
Consider a ray PA reflected at atom A in the direction AR from plane KL and another ray QB reflected at another atom B from plane MN in the direction BS. Now from the atom A, draw two perpendiculars AC and AD on the incident ray QB and reflected ray BS respectively. The path difference between these two rays is (CB+BD). The two reflected rays will be in phase or out of phase, will depend upon this path difference. When the path difference (CB+BD) is an integral multiple of the wavelength (lamda), then the |
two reflected rays will reinforce each other and produce an intense spot. Thus the condition of reinforcement is CB + BD = n (lamda)
From figure,
angle PAT = angle QTK = theta
But angle PAC = 900
So, angle TAC = 90 - theta
Now angle TAB = 900
So, as angle TAC = 90 - theta, angle CAB = theta
Now in right angled triangle ACB,
sin (angle CAB) = sin (theta) = CB / AB = CB / d
So, CB = d sin (theta).
Similarly, it can be shown that BD = d sin (theta)
So, CB + BD = 2d sin (theta) = n (lamda)
where n = 1, 2, 3 ......... etc., for first order, second order, third order ...... etc., maxima respectively. This relation is known as Bragg's law.
Bragg's law is a necessary but not sufficient condition for diffraction. It specifies the diffraction for primitive unit cells such as simple cubic cells. If the given natural crystal is nonprimitive cell, some of the diffractions predicted by Bragg's law do not occur.
Miller indices are the reciprocals of the intercepts, made by the plane on the crystallographic axes, when reduced to smallest integers.
Miller indices are used to designate the planes in a crystal lattice.
Let dhkl represent the distance between two adjacent parallel planes having Miller indices (hkl). Let the plane ABC be one of the planes. The perpendicular ON in figure from the origin to the plane ABC is equal to dhkl. Let ON makes angles alpha, beta and gama with x, y and z axes respectively. The intercepts of the plane ABC on the coordinate axes x, y and z are OA, OB and OC respectively.
Intercepts made by plane ABC on coordinate axes = OA, OB, OC
Reciprocals of these intercepts are = 1/OA, 1/OB, 1/OC
Taking LCM, we get a/OA, a/OB, a/OC
So Miller indices h = a/OA, k = a/OB, l = a/OC

|
i.e. intercepts OA = a/h, OB = a/k, OC = a/l. |
So (dhkl)2 = d2 = d2 cos2(alpha) + d2 cos2(beta) + d2 cos2(gama)
i.e. cos2(alpha) + cos2(beta) + cos2(gama) = 1 ……… (1)
The points N and A lie in the plane ABC and ON is perpendicular to plane ABC. So ON is perpendicular to NA.
Now consider right angled triangle ONA. Here angle ONA is 90 degrees.
So, here cos (alpha) = d/OA = dh/a
Similarly cos (beta) = dk/a and cos (gama) = dl/a.
So, putting these values in equation (1), we get
(dh/a)2 + (dk/a)2 + (dl/a)2 = 1
i.e. [d2/a2] ( h2 + k2 + l2 ) = 1
i.e. d2 = a2/ ( h2 + k2 + l2 )
i.e. dhkl = a / [square root of ( h2 + k2 + l2)]
2d sin (theta) = n (lamda),
where d is the interplaner distance, (theta) is the angle between the Bragg plane and the direction of the incident beam and n = 1, 2, 3 ......... etc., for first order, second order, third order ...... etc., maxima respectively, is known as Bragg's law.
Let us consider a set of parallel lattice planes of a crystal seperated by a distance d apart, i.e. AB = d. Suppose a narrow beam of X-rays of wavelength (lamda) be incident upon these planes at an angle (theta) as shown in figure. The beam will be reflected in all directions by the atoms of various atomic planes. Because the refractive index of the matter of the crystal is very nearly equal to unity, there is practically no bending of the rays entering or leaving the crystal.

|
Consider a ray PA reflected at atom A in the direction AR from plane KL and another ray QB reflected at another atom B from plane MN in the direction BS. Now from the atom A, draw two perpendiculars AC and AD on the incident ray QB and reflected ray BS respectively. The path difference between these two rays is (CB+BD). The two reflected rays will be in phase or out of phase, will depend upon this path difference. When the path difference (CB+BD) is an integral multiple of the wavelength (lamda), then the |
two reflected rays will reinforce each other and produce an intense spot. Thus the condition of reinforcement is CB + BD = n (lamda)
From figure,
angle PAT = angle QTK = theta
But angle PAC = 900
So, angle TAC = 90 - theta
Now angle TAB = 900
So, as angle TAC = 90 - theta, angle CAB = theta
Now in right angled triangle ACB,
sin (angle CAB) = sin (theta) = CB / AB = CB / d
So, CB = d sin (theta).
Similarly, it can be shown that BD = d sin (theta)
So, CB + BD = 2d sin (theta) = n (lamda)
where n = 1, 2, 3 ......... etc., for first order, second order, third order ...... etc., maxima respectively. This relation is known as Bragg's law.
GIVEN :-
r = 1.746 A0 = 1.746 x 10-10 m.
For FCC, a = 2 (square root of 2) r
i.e. a = 2 x 1.414 x 1.746 x 10-10 m
i.e. a = 4.94 x 10-10m
Spacing of (hkl) plane = dhkl = [a / square root of ( h2 + k2 + l2 )]
So, spacing of (202) plane = d202 = [ 4.94 x 10-10 / square root of ( 22 + 02 + 22 )]
i.e. d202 = 1.75 x 10-10m.
So, spacing of (220) plane = d220 = [ 4.94 x 10-10 / square root of ( 22 + 22 + 02 )]
i.e. d220 = 1.75 x 10-10m.
So, spacing of (111) plane = d111 = [ 4.94 x 10-10 / square root of ( 12 + 12 + 12 )]
i.e. d111 = 1.01 x 10-10m.
The number of equidistant neighbours that an atom has in the given structure, is the coordination number.
When the coordination number is large, the structure is more closely packed.
2d sin (theta) = n (lamda),
where d is the interplaner distance, (theta) is the angle between the Bragg plane and the direction of the incident beam and n = 1, 2, 3 ......... etc., for first order, second order, third order ...... etc., maxima respectively, is known as Bragg's law.
Let us consider a set of parallel lattice planes of a crystal seperated by a distance d apart, i.e. AB = d. Suppose a narrow beam of X-rays of wavelength (lamda) be incident upon these planes at an angle (theta) as shown in figure. The beam will be reflected in all directions by the atoms of various atomic planes. Because the refractive index of the matter of the crystal is very nearly equal to unity, there is practically no bending of the rays entering or leaving the crystal.

|
Consider a ray PA reflected at atom A in the direction AR from plane KL and another ray QB reflected at another atom B from plane MN in the direction BS. Now from the atom A, draw two perpendiculars AC and AD on the incident ray QB and reflected ray BS respectively. The path difference between these two rays is (CB+BD). The two reflected rays will be in phase or out of phase, will depend upon this path difference. When the path difference (CB+BD) is an integral multiple of the wavelength (lamda), then the |
two reflected rays will reinforce each other and produce an intense spot. Thus the condition of reinforcement is CB + BD = n (lamda)
From figure,
angle PAT = angle QTK = theta
But angle PAC = 900
So, angle TAC = 90 - theta
Now angle TAB = 900
So, as angle TAC = 90 - theta, angle CAB = theta
Now in right angled triangle ACB,
sin (angle CAB) = sin (theta) = CB / AB = CB / d
So, CB = d sin (theta).
Similarly, it can be shown that BD = d sin (theta)
So, CB + BD = 2d sin (theta) = n (lamda)
where n = 1, 2, 3 ......... etc., for first order, second order, third order ...... etc., maxima respectively. This relation is known as Bragg's law.
The packing density (PD) in SC :-
1 x (4/3) PI (R)3 / (a)3
i.e. 1/1 x 4/3 x PI/1 x [a /2]3 x 1/ (a)3
i.e. PI / 6
i.e. 0.52
i.e. percentage of packing density = 52 %
The percentage of void space in SC :-
(1 - PD) x 100
i.e. (1 - 0.52) x 100 = 48%
The packing density in BCC :-
2 x (4/3) PI (R)3 / (a)3
i.e. 2/1 x 4/3 x PI/1 x [(square root of 3) x a /4]3 x 1/ (a)3
i.e. (square root of 3) x (PI / 8)
i.e. 0.68.
i.e. percentage of packing density = 68 %
The percentage of void space in BCC :-
(1 - PD) x 100
i.e. (1 - 0.68) x 100 = 32%
The packing density in FCC :-
4 x (4/3) PI (R)3 / (a)3
i.e. 4/1 x 4/3 x PI/1 x [(square root of 2) x a /4]3 x 1/ (a)3
i.e. PI / (3 x square root of 2)
i.e. 0.74.
i.e. percentage of packing density = 74 %
The percentage of void space in FCC :-
(1 - PD) x 100
i.e. (1 - 0.74) x 100 = 26%
Hence the SC structure possesses minimum percentage of packing density and maximum percentage of void space among the three cubiccrystal structures.
GIVEN :-
r = 1.746 A0 = 1.746 x 10-10 m.
For FCC, a = 2 (square root of 2) r
i.e. a = 2 x 1.414 x 1.746 x 10-10 m
i.e. a = 4.94 x 10-10m
Spacing of (hkl) plane = dhkl = [a / square root of ( h2 + k2 + l2 )]
So, spacing of (111) plane = d111 = [ 4.94 x 10-10 / square root of ( 12 + 12 + 12 )]
i.e. d111 = 1.01 x 10-10m.
So, spacing of (220) plane = d220 = [ 4.94 x 10-10 / square root of ( 22 + 22 + 02 )]
i.e. d220 = 1.75 x 10-10m.
So, spacing of (200) plane = d200 = [ 4.94 x 10-10 / square root of ( 22 + 02 + 02 )]
i.e. d200 = 2.47 x 10-10m.
Now we have to draw (112) plane. Let intecepts by this plane on x, y and z axes are OA, OB
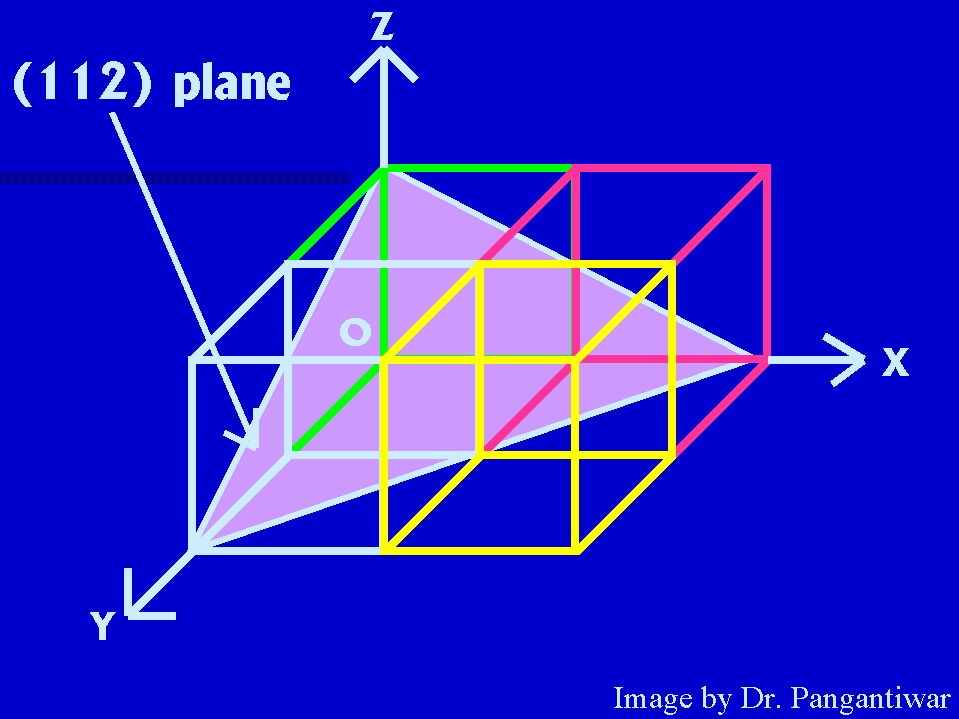
|
and OC. The reciprocals of intercepts :- 1/OA, 1/OB, 1/OC Reciprocals are reduced to smallest set of integers by taking LCM :- a/OA, a/OB, a/OC But, miller indices of this plane are:- 1, 1, 2 So, 1 = a/OA, 1 = a/OB, 2 = a/OC So, OA = a, OB = a and OC = a/2. or, OA = 2, OB = 2 and OC = 1. |
Now we have to draw (120) plane. Let intecepts by this plane on x, y and z axes are OA, OB

|
and OC. The reciprocals of intercepts :- 1/OA, 1/OB, 1/OC Reciprocals are reduced to smallest set of integers by taking LCM :- a/OA, a/OB, a/OC But, miller indices of this plane are:- (1,2,0) So, 1 = a/OA, 2 = a/OB, 0 = a/OC So, OA = a, OB = a/2 and OC = infinity i.e plane is parallel to z axis. i.e. OA = 2a, OB = 1a and plane is parallel to z axis. or, OA = 2, OB = 1 and plane is parallel to z axis. |
GIVEN :-
r = 0.1278 nm = 0.1278 x 10-9 m.
For FCC, a = 2 (square root of 2) r
i.e. a = 2 x 1.414 x 0.1278 x 10-9 m
i.e. a = 3.61 x 10-10m
Spacing of (hkl) plane = dhkl = [a / square root of ( h2 + k2 + l2 )]
So, spacing of (111) plane = d111 = [ 3.61 x 10-10 / square root of ( 12 + 12 + 12 )]
i.e. d111 = 2.08 x 10-10m.
So, spacing of (321) plane = d321 = [ 3.61 x 10-10 / square root of ( 32 + 22 + 12 )]
i.e. d321 = 9.65 x 10-11m.
|
Sr. No. |
Properties |
Unit Cell |
||
|
SC |
BCC |
FCC |
||
|
1 |
No. of atoms per unit cell, n |
1 |
2 |
4 |
|
2 |
Atomic radius, r |
a/2 |
[a (square root of 3)] / 4 |
a / [ 2 (square root of 2)] |
|
3 |
Nearest neighbour distance, 2r |
a |
[a (square root of 3)] / 2 |
a / (square root of 2) |
|
4 |
Coordination number, CN |
6 |
8 |
12 |
|
5 |
Atomic packing fraction, APF |
(Pi / 6) = 0.52 |
[Pi (square root of 3)] / 8 = 0.68 |
Pi / [3 (square root of 2)] = 0.74 |
|
6 |
Void space |
48 % |
32 % |
26 % |
|
7 |
Density |
M / [n (a)3] |
2 M / [n (a)3] |
4 M / [n (a)3] |
Let us consider a set of parallel lattice planes of a crystal seperated by a distance d apart, i.e. AB = d. Suppose a narrow beam of X-rays of wavelength (lamda) be incident upon these planes at an angle (theta) as shown in figure. The beam will be reflected in all directions by the atoms of various atomic planes. Because the refractive index of the matter of the crystal is very nearly equal to unity, there is practically no bending of the rays entering or leaving the crystal.

|
Consider a ray PA reflected at atom A in the direction AR from plane KL and another ray QB reflected at another atom B from plane MN in the direction BS. Now from the atom A, draw two perpendiculars AC and AD on the incident ray QB and reflected ray BS respectively. The path difference between these two rays is (CB+BD). The two reflected rays will be in phase or out of phase, will depend upon this path difference. When the path difference (CB+BD) is an integral multiple of the wavelength (lamda), then the |
two reflected rays will reinforce each other and produce an intense spot. Thus the condition of reinforcement is CB + BD = n (lamda)
From figure,
angle PAT = angle QTK = theta
But angle PAC = 900
So, angle TAC = 90 - theta
Now angle TAB = 900
So, as angle TAC = 90 - theta, angle CAB = theta
Now in right angled triangle ACB,
sin (angle CAB) = sin (theta) = CB / AB = CB / d
So, CB = d sin (theta).
Similarly, it can be shown that BD = d sin (theta)
So, CB + BD = 2d sin (theta) = n (lamda)
where n = 1, 2, 3 ......... etc., for first order, second order, third order ...... etc., maxima respectively. This relation is known as Bragg's law.
X-ray diffraction technique can be used to analyze different types of crystal structures using Bragg's X-ray spectrometer.
GIVEN :-
Edge of unit cell, a = 4.3 A0 = 4.3 x 10-10 m
Density of sodium, Density = 963 kg / m3
Atomic weight, M = 23 kg / k. mol
Avogadro's number, N = 6.02 x 1026 atoms / k. mol.
Density = nM / N (a)3
So, n = [Density N (a3)] / M
i.e. n = [(963 kg / m3) (6.02 x 1026 atoms / k.mol) (4.3 x 10-10m)
i.e. n = 46.09 / 23 atoms = 2 atoms
As, number of atoms per unit cell in BCC is 2, sodium crystallizes in a BCC cell.