The Schrodinger time dependent wave equation for matter wave is given by
[-{(h-cros)2 / 2m}(del)2 + V] psi = i (h-cros) d(psi)/dt (a)
The classical differential equation of a wave motion is given by
d2(psi) / dt2 = v2 (del)2 (psi)
The solution of this equation gives (psi) as a periodic displacement in terms of time i.e.,
(psi) (x,y,z,t) = (psi)0 (x,y,z) e-iwt
differentiating we get,
d (psi) / dt = -iw (psi)0 e-iwt
i.e., d (psi) / dt = -i 2 (pi) (freq.) (psi)
i.e., d (psi) / dt = -[i 2 (pi) E / h] (psi)
i.e., i (h-cros) d (psi) / dt = E
putting this value in equation (a), we get, Shrodinger's time independent wave equation of matter wave as,
[-{(h-cros)2 / 2m}(del)2 + V] psi = E (psi)
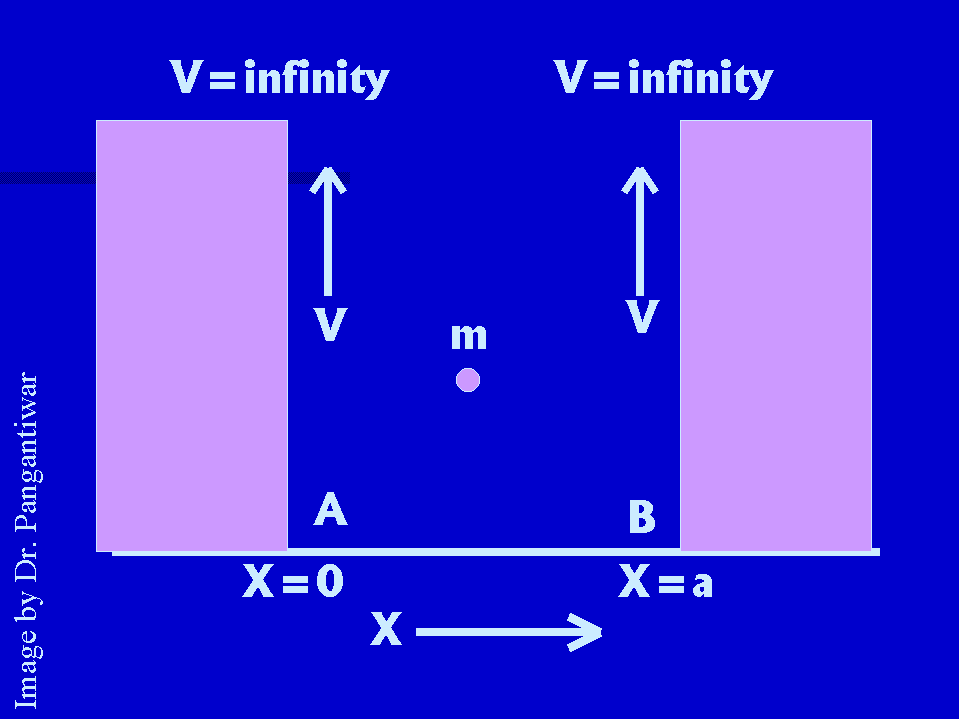
Let us consider the case of a particle of mass m moving along x axis between the two rigid walls A and B at x = 0 and x = a. The particle is free to move between the walls. The potential of the
|
particle between the two walls is constant because no force is acting on the particle. The constant potential energy is taken as zero for simplicity.When the particle strikes any one of the walls, it is reflected back immediately as the walls are perfectly rigid. Thus the potential energy of the particle becomes infinite at the walls. Thus the potential function is defined in the following way :
V(x) = infinity for x < 0 and x > a
and V(x) = 0 for 0 < x < a .....(1)
|
The Schrodinger wave equation for the particle is given by
d2(psi)/dx2 + [8 (pi)2m/h2](E - V)(psi) = 0
As V = 0 between the walls, hence the equation has the following form
d2(psi)/dx2 + [8 (pi)2m/h2] E (psi) = 0 .....(2)
Let [8 (pi)2m/h2] E = k2, then equation (2) takes the form
d2(psi)/dx2 + k2 (psi) = 0 .....(3)
The solution of second order differential equation (3) is given by
psi (x) = C eikx + D e-ikx
i.e. psi (x) = C [sin kx + i cos kx] + D [ sin kx - i cos kx]
i.e. psi (x) = [C + D] sin kx + i [C - D] cos kx
i.e. psi (x) = A sin kx + B cos kx .....(4)
where A & B are constants. The values of these constants can be obtained by applying the boundary conditions of the problem. Here the particle is enclosed between two rigid walls and we know that (psi)2 represents the probability of finding the particle at any instant.
Applying the first boundary condition, psi (x) = 0 at x = 0, we get
0 = B,
So, wave function i.e. equation (4) reduces to form
psi (x) = A sin kx .....(5)
Now, applying the second boundary condition, psi (x) = 0 at x = a, we get
0 = A sin ka,
i.e. either A is 0 or sin ka is zero,
But as B is already zero, A also can not be zero, because in that case wave function does not exist, means there can not be a particle in the infinite potential well,
So, sin ka = 0,
i.e. ka = n (pi), where n = 0, 1, 2, 3, ...............etc.
So, k = n (pi) / a
We know that, [8 (pi)2m/h2] E = k2
So, [8 (pi)2m/h2] E = k2 = n2 (pi)2 / a2
i.e. En = n2 h2 / 8 m a2, where n = 1,2,3 .....
Here n can not take zero value, because in that case wave function does not exist, that means particle can not be there in infinite potential well
So, when n = 1, E1 = h2 / 8 m a2
When n = 2, E2 = 4 h2 / 8 m a2
When n = 3, E3 = 9 h2 / 8 m a2
i.e. inside an infinitely deep potential well, the particle can have only discrete set of eigen values (values of energy) i.e., the energy of the particle is quantized.
==============
By :- Dr. A. W. Pangantiwar
