Miller indices are the reciprocals of the intercepts, made by the plane on the crystallographic axes, when reduced to smallest integers.

Miller indices are used to designate the planes in a crystal lattice.

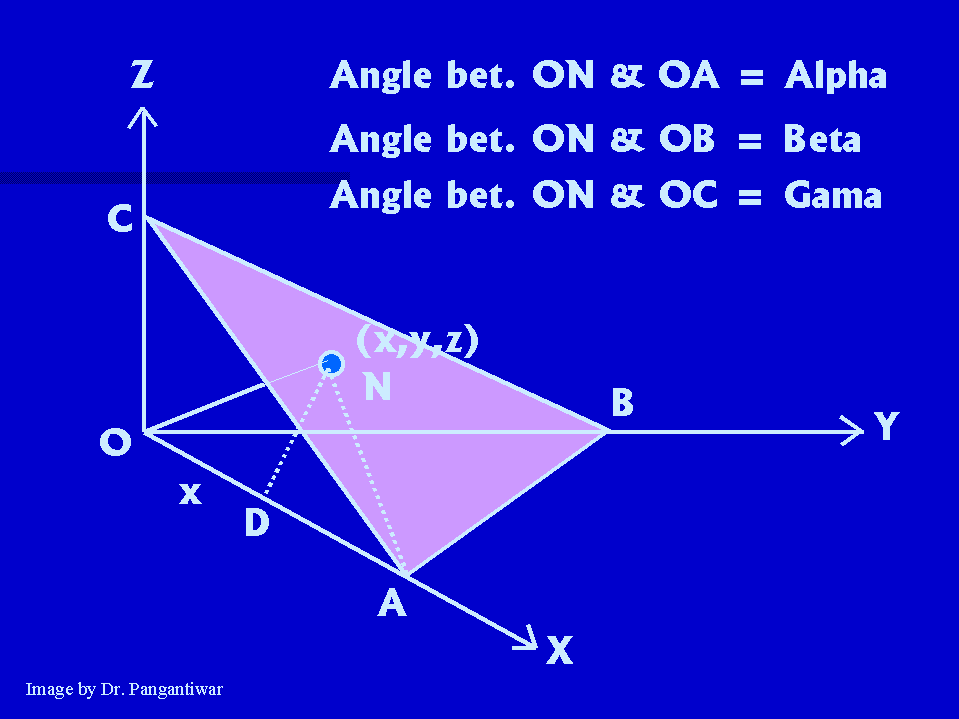
Let d_hkl represent the distance between two adjacent parallel planes having Miller indices (hkl). Let the plane ABC be one of the planes. The perpendicular ON in figure from the origin to the plane ABC is equal to d_hkl. Let ON makes angles alpha, beta and gama with x, y and z axes respectively. The intercepts of the plane ABC on the coordinate axes x, y and z are OA, OB and OC respectively.

Intercepts made by plane ABC on coordinate axes = OA, OB, OC
Reciprocals of these intercepts are = 1/OA, 1/OB, 1/OC
Taking LCM, we get a/OA, a/OB, a/OC
So Miller indices h = a/OA, k = a/OB, l = a/OC

i.e. intercepts OA = a/h, OB = a/k, OC = a/l. Let the coordinates of foot of perpendicular from O (Origin) to plane ABC i.e. point N are (x,y,z). Then (dhkl)2 = x2 + y2 + z2 In right angled triangle OND, angle NOD is 90 degrees. So cos (alpha) = x/d So x = d cos (alpha) Similarly y = d cos (beta) and z = d cos (gama).

So (d_hkl)² = d² = d² cos²(alpha) + d² cos²(beta) + d² cos²(gama)
i.e. cos²(alpha) + cos²(beta) + cos²(gama) = 1  ……… (1)

The points N and A lie in the plane ABC and ON is perpendicular to plane ABC. So ON is perpendicular to NA.
Now consider right angled triangle ONA. Here angle ONA is 90 degrees.
So, here cos (alpha) = d/OA = dh/a
Similarly cos (beta) = dk/a and cos (gama) = dl/a.

So, putting these values in equation (1), we get
(dh/a)² + (dk/a)² + (dl/a)² = 1
i.e. [d²/a²] ( h² + k² + l² ) = 1
i.e. d² = a²/ ( h² + k² + l² )
i.e. d_hkl = a / [square root of ( h² + k² + l²)]